The Beauty of Math Patterns: Exploring Mathematical Sequences
Explore the fascinating world of math patterns, from Fibonacci sequences to fractals. Read our blog to learn more.

Our expert team of math educators and enthusiasts has spent over 40 years developing and refining the most powerful teaching methods and materials into the comprehensive, industry-leading Mathnasium Method™. These “Ask Education” features are a way for the Education team members to share their knowledge and love of math with our curious readers and fans.
Hi Mathnasium! I went on a boat last weekend and my dad told me the deepest part of the lake is 540 feet and he made it sound really deep. How can I understand how deep the lake actually is? Or, even the ocean, for that matter? ~Barbara P. Grade 5
Thank you for the question, Barbara! There are over one hundred million natural lakes around the world, and their depths extend to over 5,000 feet. And yet, the depths of the world’s oceans extend more than seven times that! Scientific research reveals that the deepest point is around 36,000 feet below sea level. This point is known as the “Challenger Deep,” found in the Mariana Trench.
But you’re right, Barbara: although these are seemingly large numbers, what do they really mean to us? How do we connect a “large number” to a deeper understanding of its magnitude? Can we visualize this depth? The good news is that we can, with proportions.
A quick search online will tell you that “if Mount Everest, the highest mountain on Earth, were placed at [the Challenger Deep], it would be covered by over one mile of water.”1 This comparison already tells us that we are not alone in needing assistance to visualize the ocean’s depth. Most of us will never travel deep into the ocean to truly understand how far the bottom is, but we can compare the distance to the height of a mountain with which we are more familiar.
When two ratios are equivalent, we have a proportion. Proportions are used daily, from determining the measure of ingredients for a recipe to the amount of time a trip takes.
Both in math and the real world, we can find shapes and objects that are proportionate, meaning they have the same relative sizes. So, to better understand out-of-reach depths and distances, we can form proportions. One way to do this is with a scale factor.
A scale factor is a ratio that shows the relationship between the measurement in a drawing or model and the measurement of a real object. For example, the scale factor of a 2-foot stuffed dolphin and an 8-foot dolphin is 2:8, (reduced to 1:4), which tells us that we can visualize the length of the real dolphin with four stuffed animals lined up end to end! Using this knowledge, we can determine the scale factor of the Challenger Deep and a model of the ocean. Very simply: if we construct a model that shows the deepest point at the 6-foot mark, (roughly the height of a human being), we can visualize 6,000 human beings stacked head-to-toe to represent the depth of the Challenger Deep.
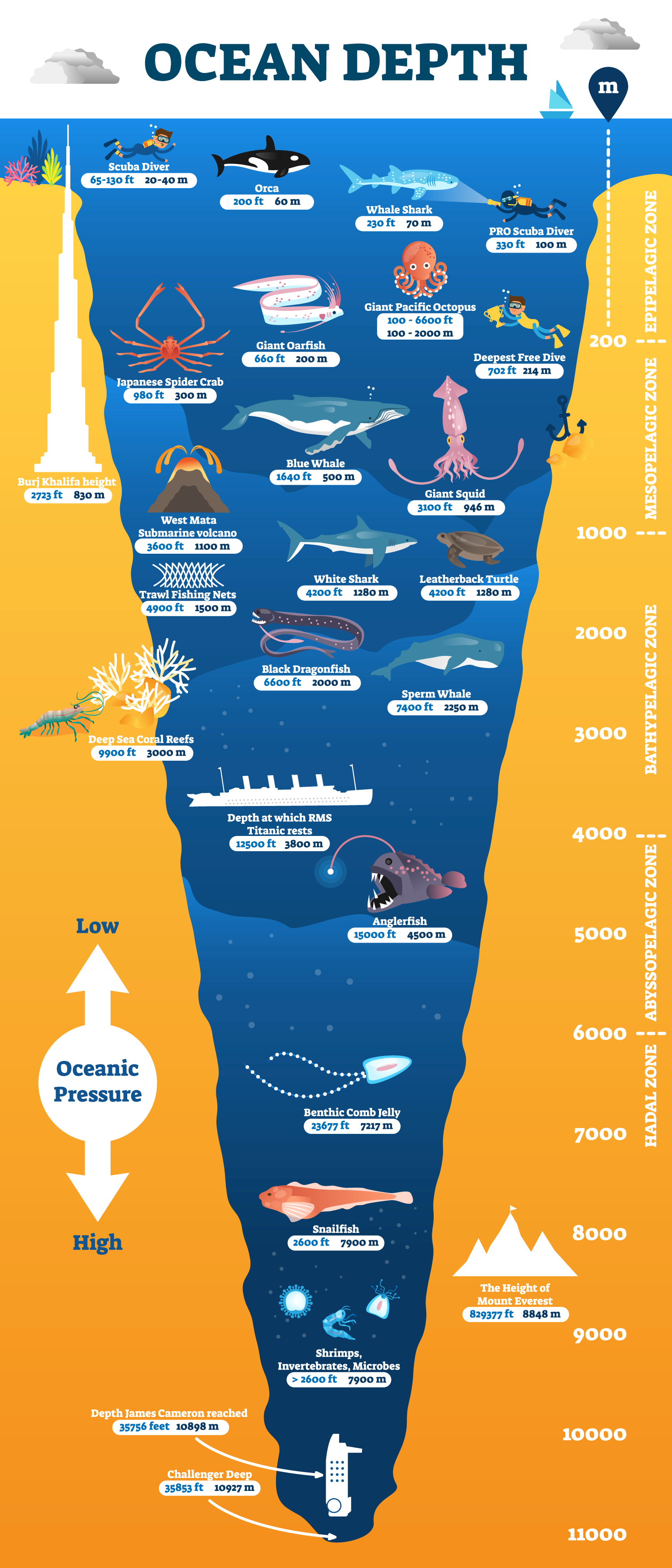
Although a 6-foot model is a great starting point, you can make the visualization a lot more interesting by comparing the ocean’s depth to the length of a football field! A football field measures 360 feet from end to end, which means you can “feel” the magnitude of the ocean’s depth by walking the length of a football field 100 times!
Fun fact: Today, ocean depth is measured using sound and radar; however, this was not always the case. Long ago, “sailors would use a tool called a lead line, which was essentially a lead weight attached to a rope that is marked every 6 feet, a length called a fathom, with a rag or strip of leather. A crew member would then throw the line into the water, and once the lead weight reached the bottom, the sailor would measure and record the distance to the ocean floor using the strips on the rope.”2 Thank goodness for technological advancement!
A fascinating exercise is to take a nature walk and use proportions to determine how tall the trees are! Using an upright-standing stick as a proportionate model, you can compare the lengths of the shadows of the tree and the stick with the height of the stick to find the height of the tree. We’re sure you’ll agree: This is a lot better (and safer) than climbing a ladder and finding a long enough tape measure!
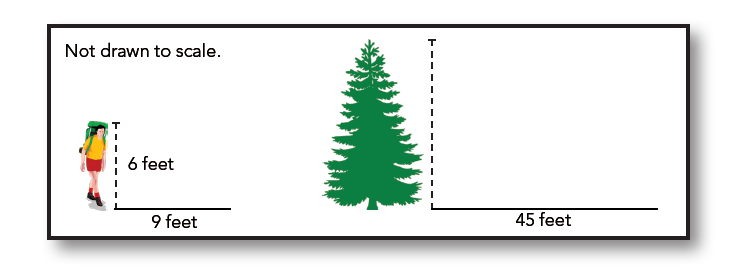
You can even use your height to help you out! For example, if an adult’s height is 6 feet and they cast a 9-foot shadow, we can calculate the height of a tree that casts a 45-foot shadow. Since there are five groups of nine inside forty-five feet, we find six feet, five times to get the tree’s height of thirty feet.
Proportions are used everywhere and are incredibly valuable. In addition to understanding the ocean’s depth, they help astronomers better understand the enormity of our galaxy and the distances and sizes of planets and stars.
Now it’s your turn, Barbara! We challenge you to take the 540-foot depth of the lake and find a comparison that helps YOU comprehend how deep it truly is. And to all our readers, we encourage you to take your own “proportion” walk around your neighborhood and see what comparisons you can make.
If you are curious to learn more about proportions, reach out to your nearest Mathnasium Learning Center. We look forward to seeing you here again soon for our next Ask Education blog post.
Readers: Do YOU have a math-related question you’d like our education team to answer? Submit it at: http://bit.ly/AskMathnasiumEducation.
Sources:
Geology.com. Deepest Part of the Ocean. Retrieved from https://geology.com/records/deepest-part-of-the-ocean.shtml
National Institute of Standards and Technology. (2022). How Do You Measure It? How Do You Measure the Depth of the Ocean? Retrieved from: https://www.nist.gov/how-do-you-measure-it/how-do-you-measure-depth-ocean


Mathnasium meets your child where they are and helps them with the customized program they need, for any level of mathematics.
