Welcome to Mathnasium’s Math Tricks series. Today we are comparing fractions to the benchmark number, one half.
When comparing fractions, it can be difficult to determine whether they represent values that are greater than or less than one another. It might be helpful to identify whether they are greater than or less than one half. To do so, we find how many parts make one half of each whole, and then we compare the number of parts to the half.
Follow the example below to arrange the fractions in order.
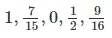
Step 1: Determine the smallest number and largest number. Since the fractions are proper fractions, they are all greater than 0 and less than 1.
Smallest: 0
Largest: 1
Step 2: Group the remaining numbers as less than half, greater than half, or equal to half.
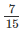is less than half.
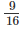is greater than half.
Answer: The numbers arranged in order are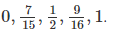 
Now, with this strategy, you are ready to compare fractions using the benchmark of one-half. Click here for more practice problems, then check your answers here.
If you missed this or any of our other Math Tricks videos, check them out on our YouTube channel!
Mathnasium meets your child where they are and helps them with the customized program they need, for any level of mathematics.
877-601-6284
877-601-6284
