Mathnasium #MathTricks: Fractions (Comparing Fractions Part 4)

Welcome to Mathnasium’s Math Tricks series. Today we are comparing fractions using the concept of wholes and parts … in this case, finding the missing parts that make one whole.

To compare fractions, we can turn to a few tricks we’ve covered in our series: comparing common denominators or same numerators, or comparing the fractions to the benchmark of one half. When these tricks do not apply, we can compare fractions to the benchmarks one whole, or zero. The trick is to find the “missing pieces” (or parts), of each fraction that make one whole, and compare these pieces — the fraction with the smallest missing piece is bigger (i.e., closer to one whole), or conversely, the fraction with the larger missing piece is smaller (i.e., closer to zero).

Note that:

• As the size of the missing piece increases, the value of the fraction becomes smaller.
• As the size of the missing piece decreases, the value of the fraction grows bigger.

Follow the example below to identify the fraction with the biggest value.

Example: You love pie! Which fractional amount of pie do you want?

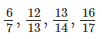
Step 1: Identify what you are looking for. You love pie and so you want the biggest piece.

Step 2: Identify the number of pieces you are comparing. You are comparing one missing piece from each pie: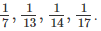

Step 3: Compare the missing pieces. Seventeenths are smaller than sevenths, thirteenths, and fourteenths.

Answer: You want 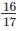of a pie, since 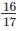is bigger than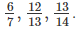

Now, with this strategy, you are ready to compare fractions by finding the missing piece that makes one whole. Click here for more practice problems, then check your answers here.

If you missed this, or any of our other Math Tricks videos, check them out on our YouTube channel!